计算模型

以下三种计算模型是等价的：

• 图灵机
• 寄存器机
• Lambda 演算

图灵机

图灵机组成

• 两端无限的线性带（读写介质）
• 有限的符号表（表示信息）
• 有限的信息处理状态
• 信息处理动作（静止，左、右移，擦写）
• 信息处理方法（状态转移规则）

定义

图灵机 $M = (Q, \Sigma, \Gamma, \delta, B, q_0, F)$，其中：

• $Q$：状态的有限集合
• $\Sigma$：有限字母表，输入符号集
• $\Gamma$：线性带符号集，显然 $\Sigma \subseteq \Gamma$
• $B$ 为空符号，可以认为是一个特殊符号因此单列。$B \in \Gamma$，$B \notin \Sigma$
• $q_0 \in Q$：初始状态
• $F \subseteq Q$：终止状态集
• $\delta$：转移函数 $Q \times \Gamma \to Q \times (\Gamma \times {L, R, S})$，其中 $L, R, S$ 代表（读写头）左右移和保持不动。
  转移函数代表了读写头的操作，包括移动和擦写动作。

例1：$\delta(q, a) = (p, (b,L))$

解释：若当前状态为 $q$，读写头读取 $a$；经过 $\delta$ 转换后，图灵机状态改为 $p$，线性带上 $a$ 改变为 $b$，同时读写头左移一格。

例2：$\delta(q, a) = (p, (a,S))$

解释：若当前状态为 $q$，读写头读取 $a$；经过 $\delta$ 转换后，图灵机状态改为 $p$，线性带上 $a$ 保持不变，同时读写头不动。

例3：$\delta(q, a) = (q, (B,R))$

解释：若当前状态为 $q$，读写头读取 $a$；经过 $\delta$ 转换后，图灵机状态不变，线性带上 $a$ 被清空，同时读写头右移一格。

图灵机的表示

可以用图或者表格。图的表示法类似有限自动机。

表格表示如下：

$\delta$	0	1	B
$q_0$	$(q_0, 0 ,R)$	$(q_1, 1 ,R)$	-
$q_1$	$(q_1, 0 ,R)$	-	$(q_2, B ,R)$
$q_2$	-	-	-

其中，第一行代表当前读写头读取的内容，第一列代表当前状态，表格内容代表转换函数。“-”代表不可能存在这种情况（请务必仔细考虑）。

当然，只有表格是不够的，你需要预先规定图灵机的相关参数（如状态集合、符号集合等）。

该图灵机识别由 0 和 1 组成的且只含有一个 1 的字符串。

图灵机的格局

格局：机器的状态的表示，由当前状态、当前带内容、读写头位置有序组成。格局属于 $(\Gamma^\star \times Q \times \Gamma^\star)$。

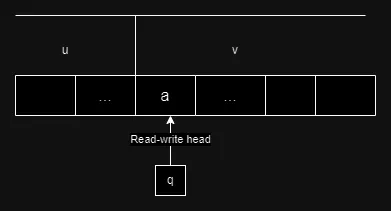
如图，该格局表示为 $(u, q, v)$，简记为 $uqv$。

显然，图灵机的初始格局为 $q_0 \omega, \omega \in \Sigma^\star$。

终止格局：$\alpha q_f \beta, (\alpha, \beta \in \Gamma^\star, q_f \in F)$。

停机格局：转换函数未定义。

格局转换：图灵机 M 根据转换函数定义合法地从格局 $C_1$ 进入格局 $C_2$，则称格局 $C_1$ 产生格局 $C_2$，称这两个格局之间有二元关系 $\vdash$，且 $C_1 \vdash C_2$。

转换关系的自反、传递闭包，即多步转换，用 $\vdash^\star$ 表示。如 $C \vdash^\star D$ 表示 $\exists C1, C_2, \cdots, C_n: C \vdash C_1, C_1 \vdash C_2, \cdots, C{n-1} \vdash C_n, C_n \vdash D$

图灵机的计算

计算：计算是从 初始格局 到 终止格局 按照动作函数规定的规则进行的一系列转换的格局转换序列。

$q_0 \omega \vdash^\star xq_fy$ 称为一个以 $\omega$ 为输入，$xy$ 为输出的计算。

例1：设计一台图灵机，接受由 0 和 1 组成的，且 0 与 1 出现次数相同，所有的 0 都在 1 前出现的字符串。如 $00 \cdots 011 \cdots 1$。

基本思路：读头将第一个 0 改为 x，右移，把找到的第一个 1 改为 y，然后退回去直到遇到第一个 x，再右移把遇到的第一个 0 改为 x，右移，把找到的第一个 1 改为 y，如此反复直至指针指向空白 B 为止。

解答：$M=({q_0, q_1, \cdots q_4}, {0, 1}, {0, 1, X, Y, B}, \delta, q_0, B, {q_4})$

如果可以完成计算，那么称为该图灵机接受输入串，否则不接受输入串。对输入串的不接受分为拒绝状态（出现定义以外的情况）和不停机状态（无法进入终止状态）。

停机分为终止状态和拒绝状态。

应用

应用实例：自然数及其运算

用输入带上连续的 0 的个数表示自然数，即 $n$ 表示为 $0^n$，函数的参数以 1 分隔。即 $f(n_1, n_2, \cdots, n_k)$ 的参数表示为：$0^{n_1} 1 0^{n_2} 1 \cdots 1 0^{n_k}$。

现在，求 $m+n$，即给定 $0^m 1 0^n$ 要求得到 $0^{m+n}$。

思路：将输入带上的中间的 1 改为 0，将最后的 0 改为 B。

图灵机的变形

• 多带图灵机
• 非确定图灵机
• 多指针图灵机
• 多维图灵机
• 离线图灵机

语言

$L(M) = {\omega \mid q_0 \omega \vdash^\star xq_fy }$ 称为图灵机 M 识别的语言。

图灵机 M 能够接受停机的所有输入信息串的集合就是 M 能识别的语言。

可识别

如果有图灵机识别一个语言，则称该语言是图灵可识别的（Turing recognizable 或者 Turing machine recognizable language）。又称为递归可枚举的（recursive enumerable）。

对于识别一个语言的图灵机，当输入为该语言的句子时，它一定进入终止状态；但当输入不是该语言的句子时，它一定不接受输入串，但不一定进入拒绝状态，有可能进入不停机状态。

可判定

如果有图灵机识别一个语言，同时对所有输入都停机，则称图灵可判定。这样的语言称为图灵可判定的。简称可判定。

这种图灵机称为判定器（decider）。

关于可判定的问题，可以阅读 关于图灵机的三个问题。

定理 1：图灵可判定语言都是图灵可识别的。

定理 2：图灵可识别的不都是图灵可判定的。

推论 1：一个语言是图灵可识别的，当且仅当有图灵机识别它。

推论 2：一个语言是可判定的，当且仅当有图灵机判定它。

通用图灵机

通用图灵机接受任意一台图灵机 M 的编码，然后模拟 M 的运作。

这要求对：

• 输入符编码
• 转换函数编码
• 图灵机编码

定理：任意一台图灵机都可以等价转换为一台通用图灵机。

Church-Turning 论题

一切直觉上能行可计算的函数都可用图灵机计算，反之亦然。

练习

1. 设计一台图灵机，接受由 a 和 b 组成的，且 a 与 b 出现次数相同的字符串.并给出一个长度大于 5 的字符串例子的计算过程。

2. 设计一台图灵机，实现自然数上的乘法，并给一实例说明计算过程。

3. 设计图灵机识别语言 ${w \mid w \in {0, 1}^\star}$ 并任给一实例说明其计算过程。

寄存器机

寄存器机是一个与图灵机等价的模型。

寄存器机是一个理想化的计算机，有助于分析算法的实际效率和进行汇编（机器编码）相关的研究。

典型的寄存器机有：

• 计数器机
• 指针机
• RAM 机
• RASP 机

RAM 机

RAM 机采用的是哈佛架构（程序不能与数据混合，是只读的，类似离线图灵机），带有间接寻址的功能。

RASP 机

采用冯诺依曼架构，不允许间接寻址。

定理：对于任意一个 RAM 机程序，存在一个等价的 RASP 机程序。证明显然。

这两个机器都与计组里面所学的类似，不再赘述。

Lambda 演算

Lambda 演算是一个形式系统，同图灵机一样可作为计算模型。Lambda 演算理论是函数式语言的基础，也是指称语义学的理论基础，可用于理论证明。

Lambda演算形式系统主要有两部分：符号系统-表达式 和 符号变换规则。

纯 Lambda 表达式

主要由变量名和抽象符号 $\lambda$、‘.’以及括号等符号构成。

用 $E$ 表示 $\lambda$ 表达式，$E$ 定义如下：

• $x$ 是变量名，则 $x$ 是 $\lambda$ 表达式。
• 若 $E_1, E_2$ 是 $\lambda$ 表达式，则 $E_1E_2$ 是 $\lambda$ 表达式。
• 若 $E$ 是 $\lambda$ 表达式，$x$ 是变量，则 $\lambda x . E$ 是 $\lambda$ 表达式。
• 若 $E$ 是 $\lambda$ 表达式，则 $(E)$ 是 $\lambda$ 表达式。

其中，$E_1E_2$ 型表达式称为应用型表达式，$\lambda x . E$ 型表达式称为抽象型表达式。

$\lambda$ 表达式的 BNF 表示（x 为变量，E 是 $\lambda$ 表达式） E ::= x | E1E2 | $\lambda$ x.E | (E)

记法约定：

• $E_1E_2 \cdots E_n \equiv ( \cdots (((E_1E_2)E_3)) \cdots ) E_n $
• $\lambda x_1. \lambda x_2. \cdots . \lambda x_n. E \equiv \lambda x_1. (\cdots (\lambda x_n. E) \cdots )$
• $\lambda x_1. \lambda x_2. \cdots . \lambda x_n. E \equiv \lambda x_1x_2 \cdots x_n. E$
• $\lambda x_1. \lambda x_2. \cdots . \lambda x_n. E1 \cdots E_n \equiv \lambda x_1. \lambda x_2. \cdots \lambda x_n.(E1\cdots En)$

作用域

设有 $\lambda$ 表达式 $\lambda x . E$，定义 $\lambda x . E$ 中的 $x$ 的作用域为其中的体表达式 $E$ 部分。

约束出现、自由出现

对变量 $x$，当它出现在表达式 $\lambda x . E$ 中时，则称 $x$ 在表达式 $\lambda x . E$ 中的出现是约束出现。若它出现的位置不被表达式约束时，则称 $x$ 在表达式中的出现是自由出现.

自由变量

若变量 $x$ 在表达式 $E$ 中是自由出现，则称变量 $x$ 为表达式 $E$ 中的自由变量。

$fv(E)$：表示表达式 $E$ 中的所有自由变量集。

• $fv(x) ={x}$
• $fv(E_1 E_2) = fv(E_1) \cup fv(E_2)$
• $fv( \lambda x.E) = fv(E) – {x}$
• $fv((E)) = fv(E)$

替换

$E[E_0/x]$ 将表达式 $E$ 中 $x$ 的自由出现用 $E_0$ 代替。

• $x[E/x]=E, y[E/x]=y$
• $(E_1 E_2)[E/x] = (E_1 [E/x])(E_2 [E/x])$
• $(\lambda x.E’)[E/x] = \lambda x. E’$
• $(\lambda y.E’)[E/x]$ 且 $x \ne y$
  • 若 $y \in fv(E)$，则 $(\lambda y.E’)[E/x] = \lambda z. E’[z/y][E/x]$（保持 $E$ 中的自由变量）
  • 否则 $(\lambda y.E’)[E/x] = \lambda y.E’[E/x]$

Lambda 变换规则

$\alpha$ 变换（换名规则）：$\lambda x.E \to_\alpha \lambda y.E[y/x]$，其中 $x \ne y$ 且 $y \notin fv(E)$

• $\lambda a.ab( \lambda a.ab) \to_\alpha \lambda a.ab( \lambda c.cb)$
• $\lambda a.ab( \lambda a.ab) \to_\alpha \lambda c.cb( \lambda a.ab)$

$\beta$ 变换（应用规则）：$( \lambda x.E) E0 \to\beta E[E_0/x]$

• $( \lambda x.xy)z \to_\beta zy$
• $( \lambda x.yz)x \to_\beta yz$
• $( \lambda x.( \lambda y.yx)z)t \to\beta ( \lambda y.yt)z \to\beta zt$
• $( \lambda x.( \lambda y.yx)z)t \to\beta ( \lambda x.zx)t \to\beta zt$

$\eta$ 变换（保值变换）：$\lambda x.Mx \to_\eta M$ 其中 $x \notin fv(M)$

• $\lambda x.(\lambda y.yyy)x \to_\eta \lambda y.yyy$
• 错误：$\lambda x.(\lambda y.yyx)x \to_\eta \lambda y.yyx$

归约基与 Lambda 归约

$\beta$ 变换和 $\eta$ 变换的左部分别称为 $\beta$ 归约基和 $\eta$ 归约基，统称为归约基。

对 Lambda 表达式 E 中的归约基按照 Lambda 变换规则进行的变换称为 Lambda 归约，简称为归约。

范式

若一 Lambda 表达式 E 中无任何归约基，则称该表达式为范式。若一个 Lambda 表达式经过有限次变换能归约成范式，则称该表达式有范式。

归约过程不唯一，计算结果可能相同也可能不同。

最左归约：依据归约基中 $\lambda$ 符号出现的顺序进行的归约称为最左归约。也称标准归约。

Church-Rosser 定理：Lambda 表达式若有范式则一定唯一，并且按最左归约一定能求到该范式。

纯 Lambda 演算实例

自然数运算

定义整数：$\lambda ab. a(a(\cdots(ab)\cdots)) = \lambda ab. a^n b$

$0 = \lambda ab. b$；$1 = \lambda ab. ab$；$2 = \lambda ab. a(ab)$

不难看出，这个定义和皮亚诺公理是等价的。

plus = $\lambda xy. \lambda ab. (x \, a)((y \, a)b)$

证明：

$\begin{aligned}
plus \; m \; n & = \lambda ab.(m \, a)((n \, a) b) \
& = \lambda ab . (\lambda ab.a^m b \, a)((\lambda ab.a^n b \, a) b) \
& \to\beta \lambda ab. (\lambda b.a^m b)((\lambda b.a^n b)b) \
& \to\eta \lambda ab. a^m(a^n b) \
& = \lambda ab. a^m a^n b \
& = \lambda ab. a^{m+n}b
\end{aligned}$

times = $\lambda xy. \lambda a. x (y a)$

留给感兴趣的同学自行证明。

证明：
$\begin{aligned} times \; m \; n & = \lambda a. m(n \, a) \\ & = \lambda a . (\lambda ab.a^m b)((\lambda ab.a^n b) a) \\ & \to_\beta \lambda a. (\lambda ab.a^m b)(\lambda b.a^n b) \\ & \to_\beta \lambda a. \lambda b. (\lambda b.a^n b)^m b \\ & \to_\beta \lambda a. \lambda b. (\lambda b.a^n b)^{m-1} a^n b \\ & \to_\beta \lambda a. \lambda b. (\lambda b.a^n b)^{m-2} a^{2n} b \\ & \cdots \\ & \to_\beta \lambda a. \lambda b. a^{mn} b \\ & = \lambda ab. a^{mn}b \end{aligned}$

逻辑运算

定义布尔值：

$T = \lambda ab. a$

$F = \lambda ab. b$

$and = \lambda xy. x \, y \, F$

$or = \lambda xy. x \, T \, y$

$not = \lambda xy. x \, F \, T$

证明：

$\begin{aligned}
and \, T \, F & = (\lambda ab.a)(\lambda ab.b)(\lambda ab.b) \
& \to\beta (\lambda b. \lambda ab. b)(\lambda ab. b) \
& \to\beta \lambda ab. b \
& = F
\end{aligned}$

更多的证明留给读者自行思考。

关系运算

定义函数 ISZERO x 的返回值为 x = 0

直接给出其 Lambda 表达式：$iszero = \lambda x . x(\lambda a. F)T$，有兴趣的读者可以自行证明。

那么小等关系（$\le$，le）即 $\lambda mn. iszero(minus \, m \, n)$

等于关系（=，eq）即 $\lambda mn. and(le \, m \, n)(le \, n \, m)$

小于关系（<，lt）即 $\lambda mn. and(le \, m \, n)(not (eq \, m \, n))$

拓展 Lambda 表达式

在纯 Lambda 表达式的基础上，加入了以下内容：

• true 和 false 是 Lambda 表达式
• 自然数 n 是 Lambda 表达式
• 函数 f 是 Lambda 表达式，f 用 Lambda 表达式定义
• 选择表达式：$E_0 \to E_1, E_2$，即当 $E_0$ 为真时结果为 $E_1$，否则为 $E_2$
• let 表达式 $let x = E_0 in E$，即用 $E_0$ 替换 $E$ 中的所有 $x$

这些拓展实际上都已经在上文定义过了，只是提供一种便捷的表示方法。

带类型的 Lambda 表达式：对于任何一个变量 $x$ 用 $\lambda x : type . E$ 的形式固定 $x$ 的类型为 type，类似 rust 的写法。

带有类型之后，就有类型系统，类似于编译中的语言系统，可以对表达式进行合法性检查。

用 $\Gamma$ 表示类型上下文，假设我们声明了一个 T 类型的变量 $x$，在表达式的上下文中就应该始终有 $x$ 是 T 类型的，也就是有该类型系统有自洽性。表示为 $\frac{x:T \in \Gamma}{\Gamma \vdash x:T}$。

如果对于表达式 $\lambda x: T_1 . E, \lambda E: T_2$，那么就应该有 $T_1 \to T_2$，也就是 $T_1$ 类型可以推出 $T_2$，表示为 $\frac{\Gamma \vdash x:T_1, \Gamma \vdash E: T_2}{\Gamma \lambda x : T . E : T_1 \to T_2}$。